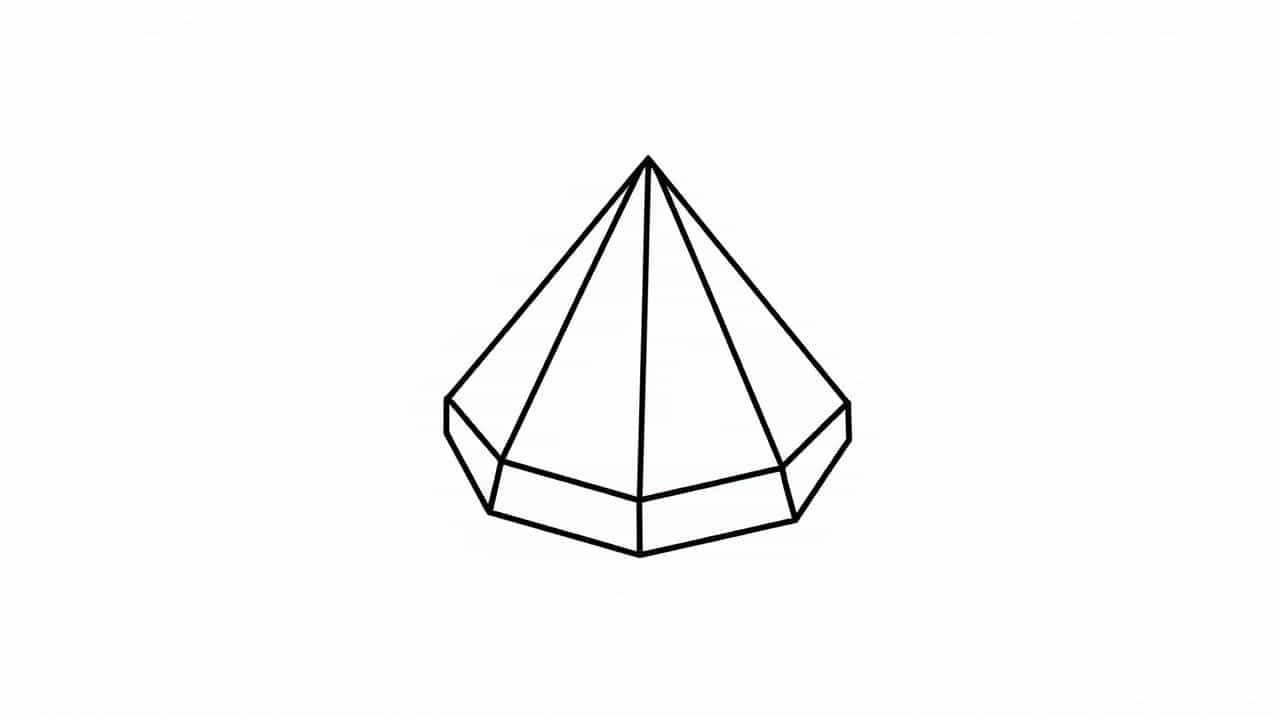
What Is an Octagonal Pyramid? A Comprehensive Guide to Its Characteristics and ApplicationsIntroductionAn octagonal pyramid is a fascinating geometric shape that appears in both theoretical mathematics and practical design. It is a three-dimensional object that has an octagonal base and triangular faces that meet at a single point, known as the apex. The octagonal pyramid is one of many types of pyramids in geometry, and its unique shape makes it an interesting object to study. This topic will dive deep into the characteristics of an octagonal pyramid, including its properties, how to calculate its surface area and volume, and some real-world applications.
Understanding the Octagonal Pyramid
An octagonal pyramid is a type of pyramid where the base is an octagon, a polygon with eight sides. Just like any other pyramid, the shape of an octagonal pyramid is defined by its base and triangular faces. The key feature of any pyramid is that all the sides of the pyramid’s faces converge at a single point above the base, called the apex.
The octagonal pyramid has the following key features:
-
Base: An octagonal polygon with eight sides.
-
Faces: Eight triangular faces, each of which connects the edges of the octagonal base to the apex.
-
Vertices: There are ten vertices – eight at the corners of the octagon and two at the apex.
-
Edges: The octagonal pyramid has 16 edges in total – eight along the base and eight connecting the apex to the vertices of the octagon.
Key Properties of an Octagonal Pyramid
An octagonal pyramid has several key properties that are important for understanding its structure and mathematical characteristics.
1. Faces
An octagonal pyramid has a total of 9 faces. The first face is the octagonal base, which is flat and lies at the bottom of the pyramid. The other eight faces are triangular and meet at the apex of the pyramid.
2. Vertices
The pyramid has 10 vertices in total:
-
8 vertices from the octagonal base, one at each corner of the octagon.
-
2 vertices at the apex, one above each of the vertices of the base, where the triangular faces converge.
3. Edges
An octagonal pyramid has 16 edges:
-
8 edges are the sides of the octagonal base.
-
8 edges connect the apex to each vertex of the octagonal base.
4. Symmetry
The octagonal pyramid has a high degree of symmetry. It has rotational symmetry, meaning it can be rotated around its central axis, and it will look the same at several positions. It also has reflectional symmetry across the vertical planes that divide the shape into equal halves.
Calculating the Surface Area of an Octagonal Pyramid
The surface area of an octagonal pyramid is the sum of the area of its octagonal base and the areas of the triangular faces. Let’s break down how to calculate the surface area step by step.
1. Area of the Base
The area A_b of the octagonal base can be calculated using the formula for the area of a regular octagon. If s is the side length of the octagon, the area A_b is given by:
Where:
-
s is the side length of the octagon.
-
a is the apothem, the distance from the center of the octagon to the middle of any side. It can be calculated using the formula:
2. Area of the Triangular Faces
The area of each triangular face can be calculated using the formula for the area of a triangle:
In the case of the octagonal pyramid, the base of each triangle is the side length of the octagonal base ( s ), and the height of each triangle is the slant height of the pyramid, denoted by l . The total area of the eight triangular faces is:
3. Total Surface Area
Finally, the total surface area A_{text{total}} of the octagonal pyramid is the sum of the area of the base and the total area of the triangular faces:
Calculating the Volume of an Octagonal Pyramid
To calculate the volume V of an octagonal pyramid, you multiply the area of the base by the height of the pyramid and then divide by 3:
Where:
-
A_b is the area of the octagonal base.
-
h is the height of the pyramid, which is the perpendicular distance from the apex to the center of the base.
Applications of the Octagonal Pyramid
The octagonal pyramid, although not as common as other shapes, has practical applications in various fields, particularly in architecture, design, and mathematics.
1. Architectural Designs
Octagonal pyramids are often used in architectural designs for creating roofs, towers, and domes. The shape provides an aesthetically pleasing appearance and a functional design. In many historical and modern buildings, the octagonal pyramid can be seen in structures such as gazebos, pavilions, and church steeples.
2. Mathematics and Geometry
In mathematics, the octagonal pyramid is used in geometry to teach students about three-dimensional shapes, surface area, and volume. It provides an excellent example of a polyhedron with a regular polygonal base and triangular faces. It also serves as a foundational concept in the study of pyramids, prisms, and other solid shapes.
3. Design and Prototyping
The octagonal pyramid is also used in industrial design and prototyping. It can be seen in the design of containers, packaging, and other objects where a stable, symmetrical shape is desired. Its unique structure allows for efficient space utilization while maintaining a distinct and visually interesting design.
4. Art and Sculpture
Artists and sculptors sometimes use the octagonal pyramid in the creation of geometric sculptures or architectural features. The symmetry and clean lines of the octagonal pyramid make it a popular choice for creating modern, abstract designs.
The octagonal pyramid is a versatile and visually appealing shape with many interesting properties. Understanding its structure, including its faces, edges, and vertices, allows for a deeper appreciation of its use in both theoretical mathematics and practical applications. Whether you are a student learning about geometric shapes or an architect incorporating unique designs into your projects, the octagonal pyramid offers an excellent example of how geometry can be applied in real-world contexts. With its symmetrical shape and stable structure, the octagonal pyramid continues to inspire and inform various fields of study and design.
“